Quadtree na Física de partículas: Uma Abordagem Computacional
Quadtree é um estrutura de dados hierárquica (em árvore) usado para organizar e dividir um espaço bidimensional em quatro regiões menores, chamadas de quadrantes. Esse processo ocorre de forma recursiva: cada nó interno da árvore se ramifica sempre em quatro filhos, enquanto os nós folha representam as regiões finais, que não precisam mais ser subdivididas. Essa estrutura é especialmente útil para armazenar, manipular e buscar dados espaciais de maneira eficiente.

Na figura acima, é apresentada uma quadtree do tipo Ponto-Região, uma estrutura que particiona o espaço com base em pontos específicos. As quadtrees podem ser classificadas de acordo com os dados que representam. Entre os tipos mais comuns, destacam-se:
- Ponto-Região: Foca na divisão do espaço com base em pontos individuais, ideal para mapear localizações ou eventos georreferenciados.
- Região: Particiona áreas contínuas, sendo útil em análises de ocupação de território ou variações de temperatura.
- Arestas: Representam contornos e formas lineares, usadas para modelar mapas de estradas ou fronteiras.
- Mapa Poligonal: Armazena polígonos e suas relações espaciais, aplicável em cartografia e sistemas de informação geográfica (SIG).
- Compactada: Agrupa regiões homogêneas para otimizar armazenamento, útil em compressão de imagens e gráficos.
Neste artigo, o foco será o tipo Ponto-região, explicando seu funcionamento e aplicações práticas.
Como a Quadtree Ponto-Região funciona?
Quadtree do tipo Ponto-região é uma estrutura que organiza o espaço bidimensional. As regiões são divididas recursivamente em quatro quadrantes iguais. Cada região (ou nó) armazena pontos específicos dentro de uma área delimitada. Quando a capacidade máxima de um nó é atingida, ele se subdivide em quatro novos nós filhos: Noroeste (NW), Nordeste (NE), Sudoeste (SW) e Sudeste (SE). Esse processo de subdivisão continua até que os nós não precisem mais ser divididos, formando os chamados nó folha.
Estrutura do nó.
A estrutura do nó é semelhante à de uma árvore binária, mas com quatro apontadores (filhos) em vez de dois. Além disso, os nós contêm informações essenciais para localizar pontos no espaço:
- Quatro apontadores: Correspondem aos quadrantes North West (NW), North East (NE), South West (SW) e South East (SE).
- Ponto: A posição do ponto armazenado.
- Chave: As coordenadas x e y do ponto.
- Valor: Metadados ou qualquer informação associada ao ponto.
Essa estrutura é amplamente usada em sistemas que lidam com grandes volumes de dados espaciais, como mapas interativos, sistemas de navegação e banco de dados georreferenciados. A simplicidade e eficiência da quadtree ponto-região o torna uma escolha muito boa para armazenar e buscar informações espaciais de forma rápida e organizada.
Aplicações práticas
| Aplicação | Descrição |
|---|---|
| Computação gráfica | Usado na compressão de imagens, armazenamento de gráficos vetoriais e representação fractal. |
| Indexação espacial | Armazena e consulta mapas geográficos e dados de terreno com eficiência. |
| Detecção de colisão | Usado em videogames e mecanismos de física para cálculos eficientes de interação de objetos. |
| Processamento de imagem | Segmentação de imagens, compressão de imagens baseada em regiões e traçado de raios baseado em quadrantes |
| Aprendizado de máquina | Acelerando pesquisas de vizinhos mais próximos em algoritmos KNN. |
Complexidade de tempo
| Operação | Complexidade |
|---|---|
| Inserir | \(O(\log_{n})\) para \(O(n)\) (depende do balanceamento e distribuição) |
| Buscar | \(O(\log_{n})\) (para árvores bem equilibradas) |
| Remover | \(O(\log_{n})\) para \(O(n)\) (pode exigir a fusão de nós) |
| Consulta de intervalo | \(O(\ k \ + \ log_{n})\) para \(O(n)\) (onde \(K\) é o número de elementos retornados) |
Quadtree e Física: O Desafio de Robbie
No laboratório de física de alta energia, Robbie, nosso robô curioso, trabalha com uma equipe de cientistas para desvendar os mistérios do universo. Durante um experimento, Gloria, uma das renomadas físicas envolvidas na pesquisa, confia em Robbie a tarefa de analisar as amostras coletadas. Ela pede que ele identifique, entre os milhares de “hits” - os pontos de interação onde partículas emergem após colisões intensas - as regiões de maior concentração e calcular a média de carga elétrica liberada nesses eventos. Robbie, ansioso para aprender mais sobre o mundo da física de partículas, aceita o desafio e começa a trabalhar em seu código.
obs: Neste artigo, usamos o conjunto de dados do experimento TrackFormers - Collision Event Data Sets. Os dados possuem 3 dimensões (x, y, z), mas para simplificar a explicação, consideramos apenas as dimensões x e y. Vale destacar que, para dados tridimensionais, a estrutura mais adequada seria uma Octree.
Para facilitar o entendimento, implementamos os exemplos em Python. No entanto, o repositório também contém implementações da Quadtree em C# e Rust. Você pode acessar o código completo no repositório do GitHub: .
Carregue as colisões de partículas detectadas
Download do dataset
import requests
import tarfile
import os
dataset_url = 'https://zenodo.org/records/14386134/files/trackml_40k-events-10-to-50-tracks.tar.gz?download=1'
local_tar_path = 'datasets/trackml_40k-events-10-to-50-tracks.tar.gz'
local_extract_path = 'datasets/trackml_40k-events-10-to-50-tracks'
if not os.path.exists('datasets'):
os.makedirs('datasets')
if not os.path.exists(local_tar_path):
print('Downloading dataset...')
with open(local_tar_path, 'wb') as f:
response = requests.get(dataset_url, stream=True)
for data in response.iter_content(chunk_size=1024):
if data:
f.write(data)
print('Extracting dataset...')
with tarfile.open(local_tar_path) as tar:
tar.extractall(local_extract_path)
print('Dataset ready!')
Downloading dataset...
Extracting dataset...
Dataset ready!
Carregue o dataset
import pandas as pd
from IPython.display import display
path = 'datasets/trackml_40k-events-10-to-50-tracks/trackml_40k-events-10-to-50-tracks.csv'
df_collisions = pd.read_csv(path)[['x', 'y', 'q', 'particle_id']]
display(df_collisions.head(10))
print(f'Total of detected particle collisions: {len(df_collisions)}')
Total of detected particle collisions: 9949945
Resultado do df_collisions

Extrair e visualizar amostras para análise
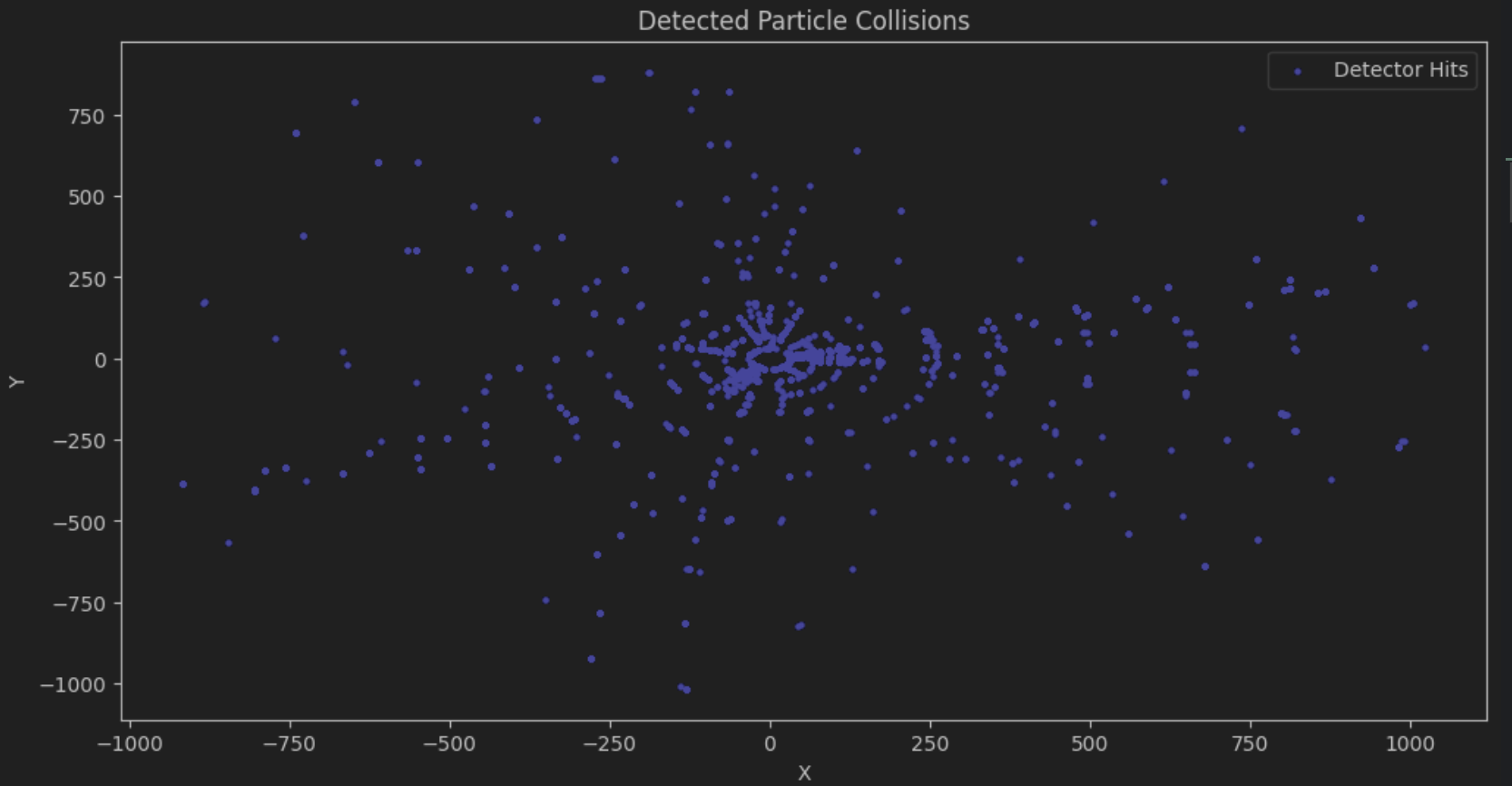
Para simplificar a análise, Robbie decide extrair uma amostra aleatória de 2000 colisões.
from helper import visualize_samples
df_samples = df_collisions[0:2000]
visualize_samples(df_samples)
Criar clusters de colisões de partículas detectadas
Criar espaço bidimensional
Robbie precisa criar um espaço bidimensional para representar as colisões de partículas detectadas. Ele começa convertendo cada colisão em um ponto no espaço, onde as coordenadas x e y representam a posição da colisão no detector.
Implementação da classe Point para representar os pontos no espaço.
from dataclasses import dataclass
@dataclass(slots=True)
class Point:
x: int
y: int
metadata: dict = None
def __repr__(self):
return f'Point({self.x}, {self.y})'
points = [Point(row.x, row.y, metadata=row.to_dict()) for index, row in df_samples.iterrows()]
points[:10]
[Point(-57.419, -67.1905),
Point(-49.4727, -58.4256),
Point(-41.6409, -49.6406),
Point(-36.2328, -43.3855),
Point(-36.4109, -43.582),
Point(-31.0184, -37.3745),
Point(-30.8612, -37.1731),
Point(-30.9992, -37.3324),
Point(-26.4289, -32.0082),
Point(-26.2202, -31.8162)]
Implementação da classe Rectangle para representar as regiões no espaço.
@dataclass(slots=True)
class Rectangle:
x: int
y: int
width: int
height: int
def contains(self, point):
return (self.x <= point.x < self.x + self.width and
self.y <= point.y < self.y + self.height)
def intersects(self, other) -> bool:
return not (other.x > self.x + self.width or
other.x + other.width < self.x or
other.y > self.y + self.height or
other.y + other.height < self.y)
def __repr__(self):
return f'Rectangle({self.x}, {self.y}, {self.width}, {self.height})'
Para criar o espaço bidimensional com as dimensões corretas, Robbie decide usar a técnica de bounding box, que é uma caixa retangular que envolve todos os pontos. Ele implementa a função compute_bounding_box que calcula a bounding box a partir de uma lista de pontos.
def compute_bounding_box(points: list) -> Rectangle:
min_x = min(p.x for p in points)
max_x = max(p.x for p in points)
min_y = min(p.y for p in points)
max_y = max(p.y for p in points)
return Rectangle(min_x, min_y, max_x - min_x, max_y - min_y)
boundary = compute_bounding_box(points)
boundary
Rectangle(-916.693, -1016.22, 1939.953, 1897.181)
Implementação da Quadtree
Robbie inicia a implementação da estrutura do Quadtree, ele define a classe Quadtree com os atributos boundary e capacity.
import numpy as np
class Quadtree:
def __init__(self, boundary: Rectangle, capacity):
self.boundary = boundary
self._capacity = capacity
self.points = np.empty((capacity, 2), dtype=np.int32)
self._metadata = np.empty(capacity, dtype=object)
self._point_count = 0
self._divided = False
self._north_east = None
self._north_west = None
self._south_east = None
self._south_west = None
def subdivide(self):
x = self.boundary.x
y = self.boundary.y
w = self.boundary.width
h = self.boundary.height
half_width = w // 2
half_height = h // 2
# Create four children that divide the current region
nw = Rectangle(x, y, half_width, half_height)
self._north_west = Quadtree(nw, self._capacity)
ne = Rectangle(x + half_width, y - half_height, half_width, half_height)
self._north_east = Quadtree(ne, self._capacity)
sw = Rectangle(x, y + half_height, half_width, half_height)
self._south_west = Quadtree(sw, self._capacity)
se = Rectangle(x + half_width, y + half_height, half_width, half_height)
self._south_east = Quadtree(se, self._capacity)
# Mark the current region as divided
self._divided = True
def insert(self, point: Point):
if not self.boundary.contains(point):
return False # Point is not in the boundary
# If there is space in the current region
if self._point_count < self._capacity: #
self.points[self._point_count] = (point.x, point.y)
self._metadata[self._point_count] = point.metadata
self._point_count += 1
return True
# If there is no space and the region is not divided
if not self._divided:
self.subdivide() # Subdivide the region if it hasn't been divided yet
# Try to insert the point into the children regions
return (self._north_west.insert(point) or
self._north_east.insert(point) or
self._south_west.insert(point) or
self._south_east.insert(point))
def insert_batch(self, points: list):
for point in points:
self.insert(point)
def query(self, boundary: Rectangle, found=None):
if found is None:
found = []
# Return if the range does not intersect the boundary
if not self.boundary.intersects(boundary):
return found
for i in range(self._point_count):
point = Point(*self.points[i], metadata=self._metadata[i])
if boundary.contains(point):
found.append(point)
if self._divided:
self._north_west.query(boundary, found)
self._north_east.query(boundary, found)
self._south_west.query(boundary, found)
self._south_east.query(boundary, found)
return found
Explicação da implementação
No construtor da classe, definimos:
- boundary: Um objeto do tipo
Rectangleque delimita a região do nó. - points: Um array NumPy pré-alocado para guardar as coordenadas dos pontos, com dimensão
(capacity, 2). - _capacity: Número máximo de pontos que o nó pode armazenar.
- _metadata: Um array para armazenar os metadados associados a cada ponto.
- _point_count: Contador de pontos inseridos.
- _divide: Flag que indica se o nó já foi subidivido.
- _north_east, _north_west, _south_east, _south_west: Nós filhos que representam os quadrantes da região.
Método subdivide()
Quando o número de pontos atinge a capacidade máxima, o método subdivide é chamado. Ele calcula a metade da largura e da altura da região atual e cria quatro novos nós-filho, cada um cobrindo uma parte do retângulo original. Essa divisão permite que pontos sejam distribuídos em regiões menores, facilitando as futuras consultas.
Método insert()
O método insert adiciona um novo ponto na Quadtree:
- Verifica se o ponto está dentro da região (boundary) do nó atual.
- Se houver espaço no nó (ou seja, point_count < capacity), o ponto e seu metadados são adicionados.
- Se não houver espaço e a região não foi dividida, a região é subdividida.
- Se a região foi dividida, o ponto é inserido em um dos nós-filho.
O método insert_batch permite inserir vários pontos de uma vez.
Método query()
O método query realiza uma busca de pontos que estejam dentro de um retângulo (a região de consulta).
- Verifica se a região de consulta intersecta a região do nó atual.
- Se houver interseção, verifica se os pontos do nó atual estão dentro da região de consulta.
- Se a região foi dividida, a busca é realizada nos nós-filho.
O resultado é uma lista de pontos (reconstruídos com seus metadados) que satisfazem a condição da consulta.
Analisar as colisões de partículas
Com a Quadtree implementado, Robbie pode iniciar a análise das colisões de partículas. Ele cria uma Quadtree com a bounding box do espaço bidimensional e insere as colisões detectadas.
quadtree = Quadtree(boundary, capacity=10)
quadtree.insert_batch(points)
Como analisar as regiões automaticamente?
Robbie se depara com um desafio: como percorrer automaticamente cada região do espaço para identificar áreas com maior densidade de colisões de partículas? Realizar esse processo manualmente, passando as coordenadas uma a uma, seria inviável, devido à vastidão do espaço e à distribuição imprevisível das regiões de interesse.
Para resolver esse problema, Robbie decide usar uma técnica de processamento de dados que automatiza a análise de diferentes áreas do espaço. Ele implementa a classe SlidingWindowQuery, que varre o espaço sistematicamente, avaliando a densidade de colisões em cada região. Essa abordagem permite identificar padrões e áreas críticas de forma eficiente e precisa.
class SlidingWindowQuery:
def __init__(self, quadtree: Quadtree):
self._quadtree = quadtree
def query(self, **kwargs):
window_size = kwargs.get('window_size', 10)
step_size = kwargs.get('step_size', window_size / 2)
density_threshold = kwargs.get('density_threshold', 3)
found = []
boundary = self._quadtree.boundary
x_start, y_start = boundary.x, boundary.y
x_end, y_end = boundary.x + boundary.width, boundary.y + boundary.height
x_values = np.arange(x_start, x_end - window_size + step_size, step_size)
y_values = np.arange(y_start, y_end - window_size + step_size, step_size)
for x in x_values:
for y in y_values:
window = Rectangle(x, y, window_size, window_size)
points = self._quadtree.query(window)
if len(points) >= density_threshold:
found.append((window, len(points), points))
return found
Explicação da implementação
A classe SlidingWindowQuery realiza uma busca em janela deslizante na quadtree, avaliando a densidade de colisões em cada região.
- Parâmetro de Consulta
No métodoqueryaceita três parâmetros configuráveis:- window_size: Tamanho da janela de busca.
- step_size: Quanto a janela se move a cada iteração.
- density_threshold: Número mínimo de pontos que a janela deve conter para ser considerada relevante.
- Definindo o Espaço de Busca:
O código usa o limite (boundary) da quadtree para saber o espaço total a ser analisado e calcula os pontos de início e fim para as janelas. - Movimentação da Janela:
Com
np.arange, uma série de valores é gerada para as coordenadas x e y, permitindo que a janela percorra todo o espaço. - Verificação em Cada Janela:
Para cada posição, é criada uma janela (um retângulo) e a quadtree é consultada para encontrar os pontos dentro dessa janela. Se o número de pontos for igual ou maior que o
density_threshold, essa janela é registrada como uma área de interesse. - Resultado: Ao final, o método retorna uma lista com as janelas relevantes, juntamente com a contagem de pontos e os próprios pontos encontrados..
Com tudo pronto, Robbie pode agora analisar as regiões de maior densidade de colisões de partículas.
window_size = 100 # Size of the window to analyze
step_size = 25 # Step size to slide the window
density_threshold = 20 # Minimum number of collisions in the window
sliding_window_query = SlidingWindowQuery(quadtree)
query_result = sliding_window_query.query(window_size=window_size,
step_size=step_size,
density_threshold=density_threshold)
display(query_result[:1])
[(Rectangle(-841.693, -416.22, 100, 100),
20,
[Point(-788, -343),
Point(-757, -336),
Point(-804, -405),
Point(-804, -405),
Point(-788, -343),
Point(-757, -336),
Point(-804, -405),
Point(-804, -405),
Point(-788, -343),
Point(-757, -336),
Point(-804, -405),
Point(-804, -405),
Point(-804, -405),
Point(-804, -405),
Point(-804, -405),
Point(-804, -405),
Point(-788, -343),
Point(-757, -336),
Point(-788, -343),
Point(-757, -336)])]
Visualizar os resultados
from src.visualization import visualize_windows_results
visualize_windows_results(quadtree, points, query_result)
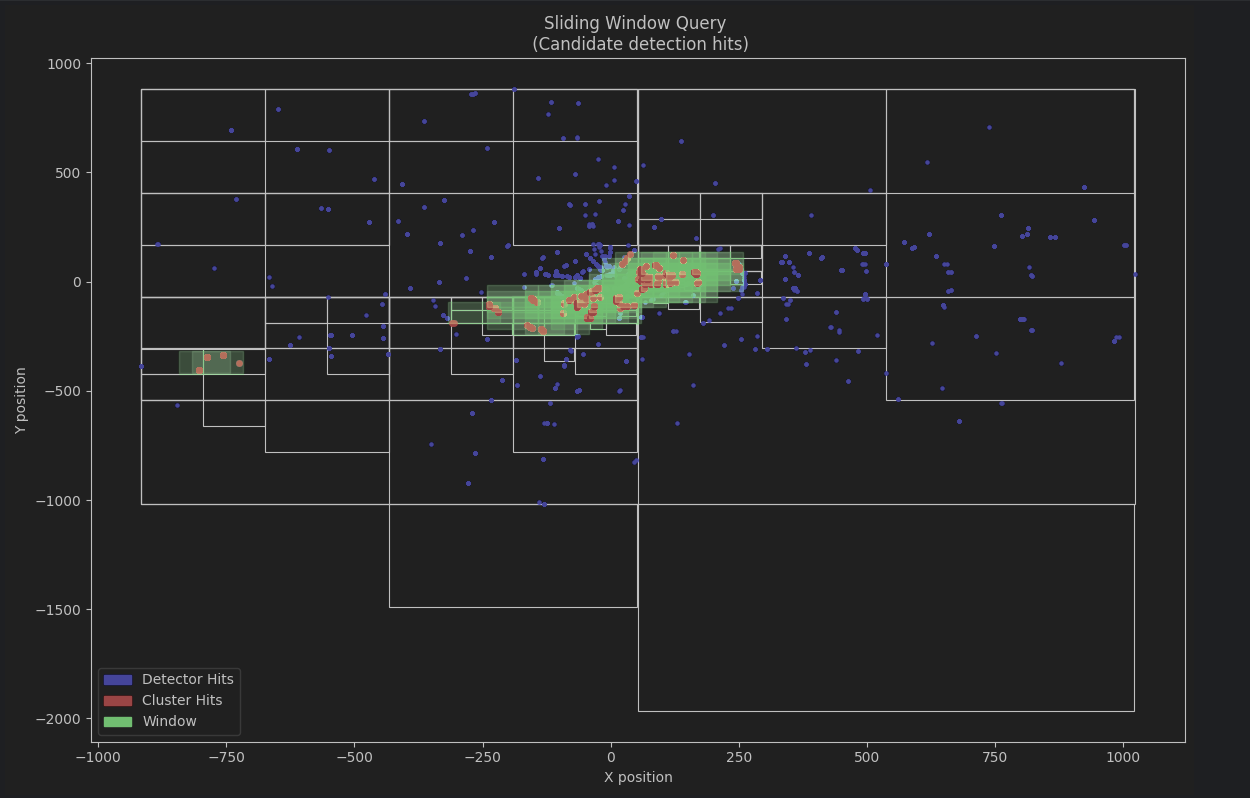
No gráfico, as áreas são subdivididas pela quadtree em retângulos, representando a organização espacial que facilita a análise localizada de colisões. A área verde simboliza a janela deslizante (sliding window), que percorre o espaço sistematicamente, analisando cada setor em busca de concentrações de colisões.
Os pontos azuis marcam os eventos detectados (Detector Hits), enquanto os pontos vermelhos indicam áreas com alta densidade de colisões (Cluster Hits), evidenciando agrupamentos onde ocorreram múltiplos impactos. As regiões com maior concentração de pontos vermelhos representam áreas de interesse para a análise, destacando padrões de colisão significativos. A varredura deslizante, combinada com a estrutura hierárquica da quadtree, permite uma análise eficiente, focando diretamente nas áreas com maior atividade, ao mesmo tempo em que otimiza o desempenho ao evitar varreduras desnecessárias em regiões de baixa densidade. Essa abordagem une precisão e eficiência para revelar padrões espaciais de colisões.
Analisando os clusters
clusters = []
for window, count, cluster_hits in query_result:
cluster = {
'coordinates': (window.x, window.y),
'particles_count': count,
'avg_particle_charge': np.mean([point.metadata['q'] for point in cluster_hits]),
'particles': [point.metadata for point in cluster_hits]
}
clusters.append(cluster)
display(pd.DataFrame(clusters))
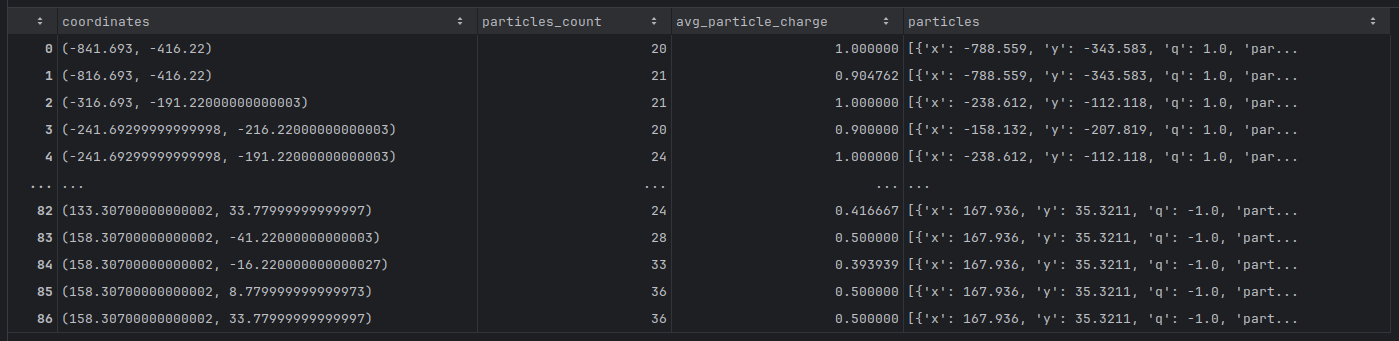
Robbie, observa os dados dos clusters e analisa a tabela obtida. Essa tabela apresenta os resultados da varredura automática que ele implementou, destacando as principais métricas de cada região examinada.
As primeiras observações de Robbie recaem sobre a coluna coordinates, que mostra as coordenadas centrais de cada área analisada, indicando os pontos específicos do espaço onde ocorreram colisões. Em seguida, ele analisa a coluna particles_count, que revela a quantidade total de partículas detectadas por região. Ao perceber variações significativas nesse número, Robbie identifica áreas de maior densidade, o que pode indicar regiões de interesse para seu estudo.
Com atenção, Robbie observa a coluna avg_particle_charge, que exibe a média das cargas elétricas das partículas detectadas. Ele nota que valores próximos de 1.0 indicam predominância de partículas positivas, enquanto valores negativos ou fracionários sugerem uma distribuição mista ou predominância de partículas negativas.
Por fim, Robbie se aprofunda na coluna particles, que contém uma lista detalhada das partículas detectadas, com suas respectivas coordenadas e cargas elétricas (q). Essa visualização granular permite que ele identifique padrões, como aglomerações de partículas com características similares, ajudando-o a compreender melhor as áreas de maior atividade no experimento.
Com essa análise, Robbie apresenta os resultados para Gloria. Ela fica impressionada com a eficiência do algoritmo e a qualidade das informações obtidas. Com esses dados em mãos, a equipe de cientistas pode agora investigar as regiões de maior densidade de colisões e identificar padrões e tendências nos dados. Isso pode levar a descobertas significativas que ajudarão a desvendar os mistérios do universo.
Conclusão
A quadtree ponto-região é uma poderosa estrutura para organização e análise de dados espaciais. Sua aplicação no estudo das colisões de partículas demonstra sua eficiência em identificar padrões e áreas críticas. Com o apoio da quadtree, Robbie e a equipe de cientistas conseguiram explorar grandes volumes de dados com rapidez e precisão, reafirmando a importância dessa estrutura em problemas complexos da ciência e da tecnologia.
Referências
- U. Odyurt e N. Dobreva. “TrackFormers - Collision Event Data Sets”. Zenodo, 2024. Link para o artigo
- Wikipedia contributors. “Quadtree.”, 2025. Wikipedia, The Free Encyclopedia, 2025 Link para o artigo
